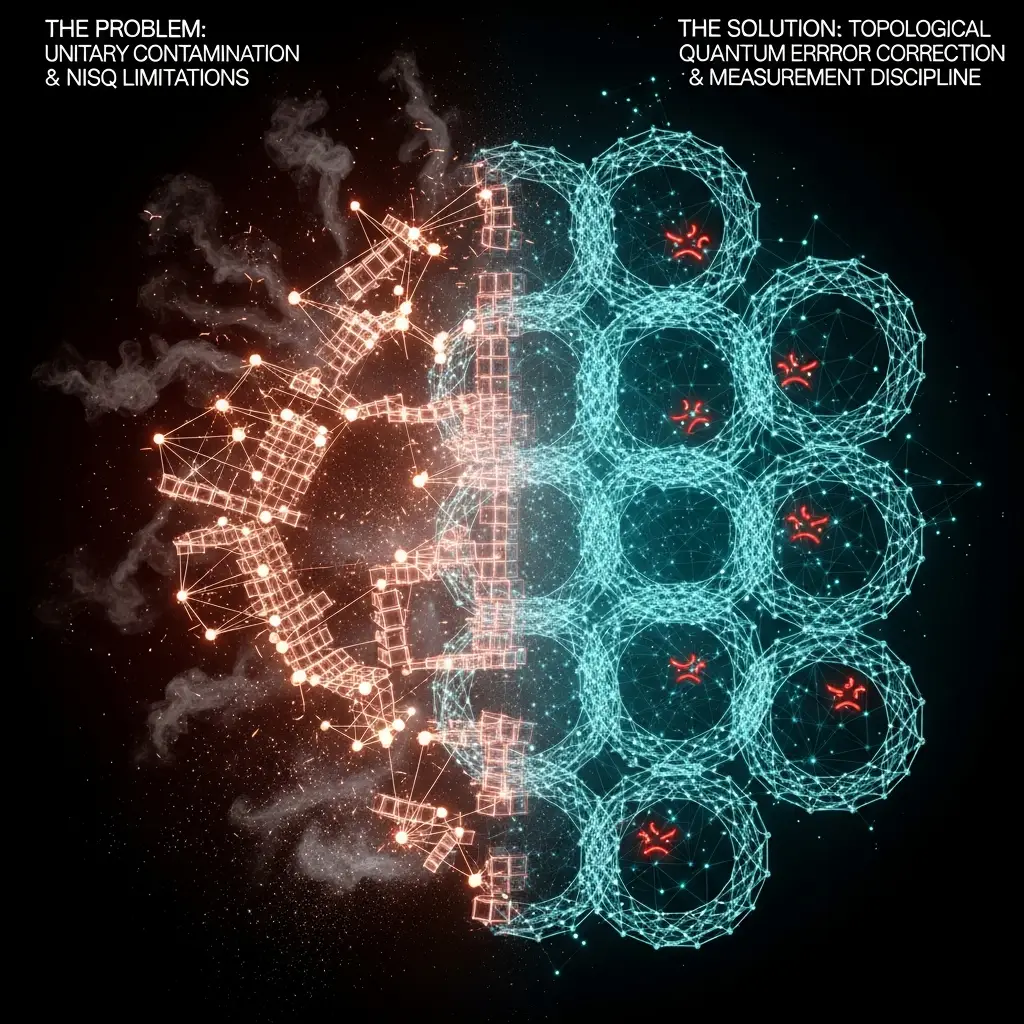
You’ve spent weeks meticulously crafting your quantum algorithm, only to watch it collapse under the weight of “Unitary Contamination.” It’s a familiar ghost in the circuit, especially when you’re pushing the limits of deep NISQ hardware. But what if the noise isn’t an insurmountable barrier, but a symptom of a deeper issue? We’re not talking about hand-waving fixes or theoretical castles in the sky; we’re diving into the gritty, hardware-optimized techniques, like topological quantum error correction, that can actually silence that ghost and bring your computation back from the brink.
Navigating the Realities of Quantum Hardware: Beyond the Topological Fantasies
Let’s be brutally honest: the academic quantum code you see splashed across colorful infographics often feels like a beautifully rendered blueprint for a city that doesn’t exist yet. The problem isn’t the elegance of the mathematics behind Shor’s algorithm or the promise of Grover’s search; it’s the brutal, unyielding reality of the hardware. We’re stuck wrestling with v5 measurement latency and qubits that seem to have a personal vendetta against coherence. This isn’t about magical future machines; it’s about squeezing every ounce of utility out of the machines we have now. If your circuit geometry is flat and your measurement discipline is an afterthought, you’re essentially inviting that ghost in for tea and expecting it to behave.
Topological Quantum Error Correction: From Theory to Practical Necessity
This is where the concept of topological quantum error correction starts to move beyond theoretical nicety and becomes a practical necessity. Forget bulky logical qubit encodings for a moment. We’re talking about leveraging the geometry of your circuit to build in resilience from the ground up. It’s about embedding computations within self-similar patterns of entangling operations and cancellations. This isn’t just about running a computation; it’s about designing the shape of the computation to actively combat noise.
Topological Quantum Error Correction: Sculpting Circuits for ECDLP Resilience
When we apply this layered approach—recursive geometric circuitry for inherent error mitigation and a disciplined measurement exclusion protocol—to a concrete, non-trivial benchmark like the Elliptic Curve Discrete Logarithm Problem (ECDLP), the results speak for themselves. Implementing Shor-style period finding with Regev-inspired, more noise-robust constructions, and mapping group operations onto these geometrically sound gate patterns, allows us to resolve ECDLP instances on current hardware that would appear “beyond reach” under standard, flat-circuit assumptions.
Architecting Resilience with Topological Quantum Error Correction
So, the next time your algorithm dissolves into a cloud of probabilistic garbage, don’t just sigh and blame the hardware. Consider the shape of your computation. Are you embedding it within a geometric structure that actively cancels errors? Are your measurement protocols designed to root out anomalies before they contaminate your results? The ghost of Unitary Contamination might be a symptom, but the cure lies in architecting resilience directly into the fabric of your quantum programs, making topological quantum error correction a tangible tool for your current hardware.
For More Check Out